Exponential decay |
Poisson distribution |
|
It is known that if we have a kilogram of Uranium-235 after
704 million years we would have 0,5 kilograms of Uranium-235 - because in that
time the nucleus of half of the atoms has disintegrated turning into Lead-207
and emitting radioactive particles – that amount of time is called half-life of the isotope.
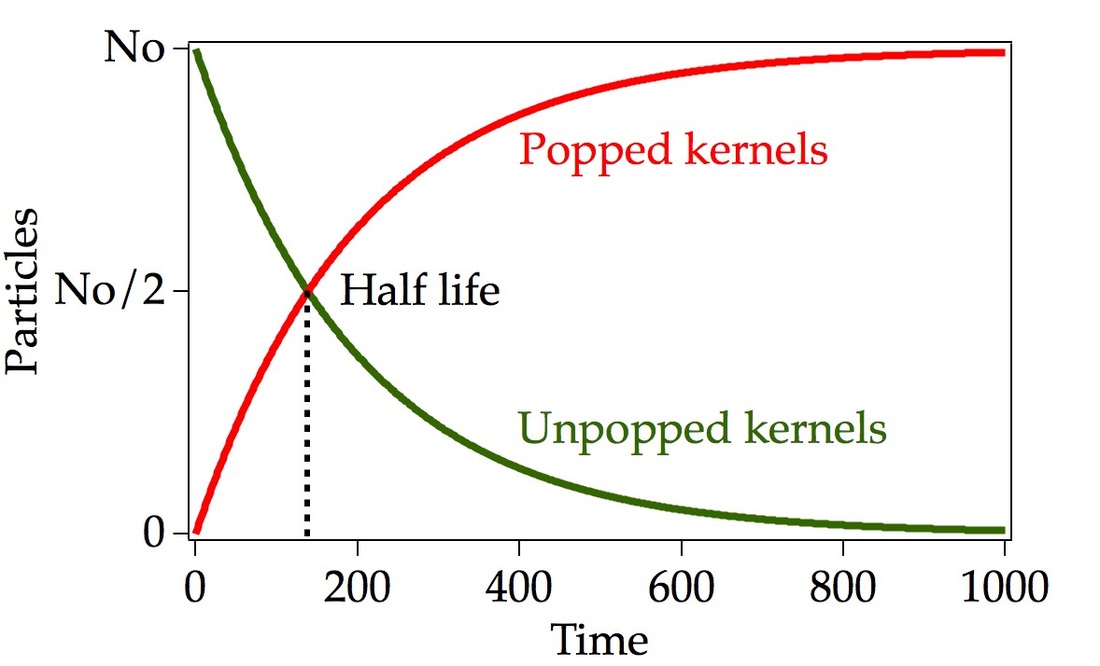
This property determines that no matter we have a ton of Uranium-235 or a milligram, after 704 million years (its half-life) we would have half of the original amount of the isotope left. Representing the percentage of atoms that disintegrate versus the
percentage of atoms that remain integer we end up with a graphic such as the
following one, which shows the exponential
decay of the isotope and where the intersection is the half-life of the isotope.
|
After studying
radioactive decay they have reached some ways to measure and analyze
radioactive decay. One concept is the half-life,
another measurement is the Poisson distribution.
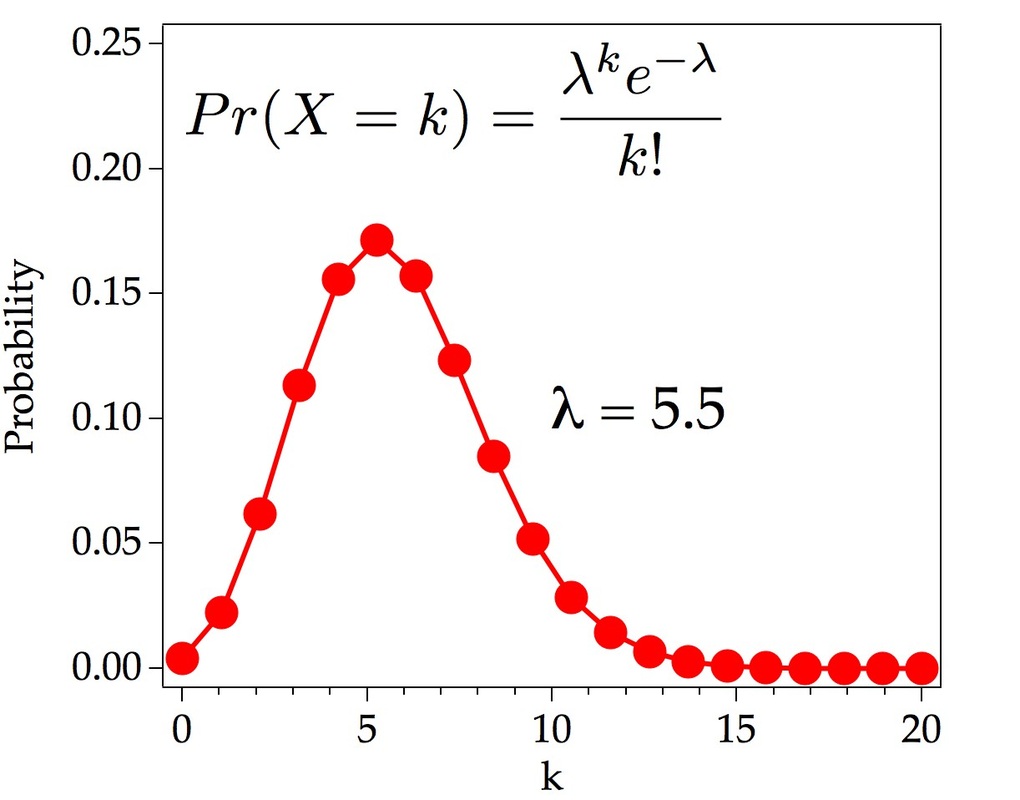
The natural phenomenon of radioactivity sticks to the Poisson distribution, which measures the number of events happening in one time unit. To be clearer, the number of kernels which pop in the same second: how many kernels pop in the first second, how many does it in the second second... and continuously until you create a graphic such as the following. It is impossible to predict whether a concrete
kernel will pop in a certain instant of time, or to guess when it will pop!
However, it is feasible to estimate how many kernels will pop in the following
instant.
|